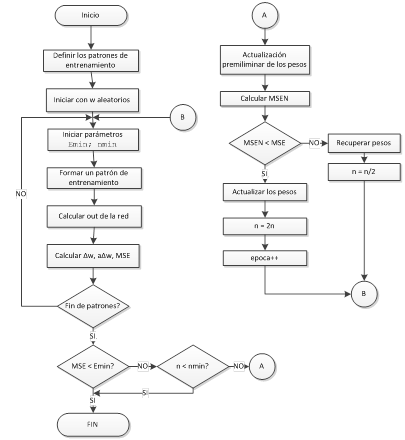
Introducción. El método de descenso más pronunciado consiste en
el siguiente procedimiento: El factor de aprendizaje es el mismo para todos los
pesos. Iniciar el factor de aprendizaje con un valor y doblarlo cada época.
Esto conduce a una actualización preliminar de los pesos. El Error medio
cuadrático MSE se calcula para los pesos actualizados que corresponden a la
tasa de aprendizaje actual. Si el MSE no decrece con esta tasa de aprendizaje,
los pesos retornan a sus valores originales, la tasa de aprendizaje se reduce a
la mitad y se continúa el entrenamiento. Si el MSE todavía no decrece, se parte
el factor de aprendizaje a la mitad repetidamente hasta encontrar una tasa de
aprendizaje que reduzca el MSE. En este punto el factor de aprendizaje es
doblado otra vez y se inicia un nuevo paso. El proceso se repite una y otra
vez. La búsqueda continúa en esta forma y termina dentro de un número
predefinido de épocas de entrenamiento. Si la disminución en el error con
respecto al paso previo es más pequeña que un nivel especificado Emin o
si el valor del factor de aprendizaje cae bajo un límite especificado
nmin el proceso se detiene.
1. De acuerdo al enunciado, dibuje un diagrama de flujo que resuelva el aprendizaje de una red neuronal por descenso más pronunciado.
2. Transcriba el código para
considerar que “El Error medio
cuadrático MSE se calcula para los pesos actualizados que corresponden a la
tasa de aprendizaje actual”. Indique como su código considera la idea de que si
el MSE no decrece los pesos deben retornar a sus valores iniciales.
Teniendo en cuenta que el
factor de aprendizaje se dobla cada época y que si el MSE no disminuye se
retorna a su aprendizaje inicial se tiene el siguiente código:
inputs=[0 0; 0 1; 1 0; 1 1];
targ=[0;1;1;0];
n=0.1
for e=1:400
sumaerr=0;
for i=1:length(targ)
………
end
errorepoca(e)=sumaerr;
n=n*2;
if e>1
&& (errorepoca(e)-errorepoca(e-1))>0
n=0.1; %Valor inicial
end
end
3. Escriba las líneas de código que
toman en cuenta la idea de que: “Si el MSE no decrece con esta tasa de
aprendizaje, los pesos retornan a sus valores originales, la tasa de
aprendizaje se reduce a la mitad y se continúa el entrenamiento. Si el MSE
todavía no decrece, se parte el factor de aprendizaje a la mitad repetidamente
hasta encontrar una tasa de aprendizaje que reduzca el MSE. En este punto el
factor de aprendizaje es doblado otra vez y se inicia un nuevo paso”
En el caso que el MSE no se reduzca se divide el factor de
aprendizaje en múltiplos de 2 de acuerdo a un contador.
inputs=[0 0; 0 1; 1 0; 1 1];
targ=[0;1;1;0];
n=0.1;cont=1;
for e=1:400
sumaerr=0;
for i=1:length(targ)
………
end
errorepoca(e)=sumaerr;
n=n*2;
if e>1
&& (errorepoca(e)-errorepoca(e-1))>0
n=0.1/(cont*2); %Aprendizaje se divide a la mitad
cont=cont+1;
end
4. Escriba el código que resuelve la idea final del
enunciado: “La
búsqueda continúa en esta forma y termina dentro de un número predefinido de
épocas de entrenamiento. Si la disminución en el error con respecto al paso
previo es más pequeña que un nivel especificado Emin o si el valor del factor de aprendizaje cae bajo un límite especificado nmin el proceso se detiene”.
El error y aprendizaje
mínimo se los definió en 0.01, también se tomó en cuenta que el factor de
aprendizaje no se dobla si no cumple con
los mínimos anteriormente mencionados.
inputs=[0 0; 0 1; 1 0; 1 1];
targ=[0;1;1;0];
n=0.1;cont=1; Emin=0.01; nmin=0.01;
for e=1:400
sumaerr=0;
for i=1:length(targ)
………
End
errorepoca(e)=sumaerr;
if e>1
&& (errorepoca(e)-errorepoca(e-1))>0
Erroractual=(errorepoca(e)-errorepoca(e-1))/errorepoca(e);
if
n>nmin && Erroractual>Emin;
n=0.1/(cont*2);
cont=cont+1;
end
end
if n>nmin && Erroractual>Emin;
n=n*2;
end
end
5. Presente los resultados obtenidos en
dos gráficos: el error en cada época y la función de la red neuronal versus las
entradas. Realice la corrida del programa por varias veces y determine la
efectividad de la convergencia: Número de veces que converge/Número de corridas.
inputs=[0 0; 0 1; 1 0; 1 1];
targ=[0;1;1;0];
alfa=4;
a01=0.2;a11=0.2;a12=0.2;a02=0.2;a21=0.2;a22=0.2;b0=0.2;b1=0.2;b2=1;
input01=1;input02=1;input03=1;n=0.1;errorepoca=0;cont=1;nmin=0.01;
Emin=0.01;
for e=1:400
sumaerr=0;
for i=1:length(targ)
y1=sigmf(input01*a01+inputs(i,1)*a11+inputs(i,2)*a21,[alfa 0]);
y2=sigmf(input02*a02+inputs(i,1)*a12+inputs(i,2)*a22,[alfa 0]);
z=sigmf(input03*b0+y1*b1+y2*b2,[alfa
0]);
deltab0=n*(targ(i)-z)*alfa*z*(1-z);
deltab1=n*(targ(i)-z)*alfa*z*(1-z)*y1;
deltab2=n*(targ(i)-z)*alfa*z*(1-z)*y2;
deltaa01=n*(targ(i)-z)*alfa*z*(1-z)*alfa*b1*y1*(1-y1);
deltaa11=n*(targ(i)-z)*alfa*z*(1-z)*alfa*b1*y1*(1-y1)*inputs(i,1);
deltaa12=n*(targ(i)-z)*alfa*z*(1-z)*alfa*b2*y2*(1-y2)*inputs(i,1);
deltaa02=n*(targ(i)-z)*alfa*z*(1-z)*alfa*b2*y2*(1-y2);
deltaa21=n*(targ(i)-z)*alfa*z*(1-z)*alfa*b1*y1*(1-y1)*inputs(i,2);
deltaa22=n*(targ(i)-z)*alfa*z*(1-z)*alfa*b2*y2*(1-y2)*inputs(i,2);
b0=b0+deltab0;
b1=b1+deltab1;
b2=b2+deltab2;
a01=a01+deltaa01;
a11=a11+deltaa11;
a12=a12+deltaa12;
a02=a02+deltaa02;
a21=a21+deltaa21;
a22=a22+deltaa22;
error=1/2*(targ(i)-z)^2; %obtiene el error
sumaerr=sumaerr+error;%suma
todos los errorres
end
errorepoca(e)=sumaerr;
if e>1
&& (errorepoca(e)-errorepoca(e-1))>0
Erroractual=(errorepoca(e)-errorepoca(e-1))/errorepoca(e);
if
n>nmin && Erroractual>Emin;
n=0.1/(cont*2);
cont=cont+1;
end
end
if n>nmin && Erroractual>Emin;
n=n*2;
end
end
%grafica
[in1,in2] = meshgrid(0:.01:1, 0:.01:1);
net1=input01*a01+in1*a11+in2*a21;
net2=input02*a02+in1*a12+in2*a22;
Gy1=1./(1+exp(-alfa*net1));
Gy2=1./(1+exp(-alfa*net2));
net=input03*b0+Gy1*b1+Gy2*b2;
Gz = 1./(1+exp(-alfa*net));
subplot(2,2,1);
mesh(in1,in2,Gz)
xlabel('in1');ylabel('in2');
subplot(2,2,2);
plot(errorepoca)
aux =
round(Gz); %Para graficar la linea de frontera
subplot(2,2,3);
mesh(in1,in2,aux)
view(0,90);xlabel('in1');ylabel('in2');
%para comprobar si funcionan los pesos
for s=1:length(targ)
y1=sigmf(input01*a01+inputs(s,1)*a11+inputs(s,2)*a21,[alfa 0]);
y2=sigmf(input02*a02+inputs(s,1)*a12+inputs(s,2)*a22,[alfa 0]);
salida(s)=sigmf(input03*b0+y1*b1+y2*b2,[alfa
0]);
end
salida