1. Grafique un perceptrón
multicapa con 2 entradas, 3 neuronas escondidas y una neurona de salida.
2. Considere una neurona con
función de activación sigmoide y dos entradas. Grafique la función de la
neurona para w0=0; w1=1; w2=0. Grafique la
línea de frontera. La línea de frontera determina el umbral de activación de la
neurona que aumenta sobre la línea y disminuye debajo de ella.
[in1,in2] = meshgrid(-5:.1:5,
-5:.1:5);
alfa=1;
w0=0;
w1=1;
w2=0;
net = w0 + in1*w1 + in2*w2;
z = 1./(1+exp(-alfa*net));
subplot(1,2,1);
mesh(in1,in2,z)
xlabel('in1');
ylabel('in2');
aux = round(z);
subplot(1,2,2);
mesh(in1,in2,aux)
xlabel('in1');
ylabel('in2');
3. Considere una neurona con
función de activación sigmoide y dos entradas. Grafique la función de la
neurona para w0=0; w1=0; w2=1. Grafique la
línea de frontera.
[in1,in2] = meshgrid(-5:.1:5,
-5:.1:5);
alfa=1;
w0=0;
w1=0;
w2=1;
net = w0 + in1*w1 + in2*w2;
z = 1./(1+exp(-alfa*net));
subplot(1,2,1);
mesh(in1,in2,z)
xlabel('in1');
ylabel('in2');
aux = round(z);
subplot(1,2,2);
mesh(in1,in2,aux)
xlabel('in1');
ylabel('in2');
4. Considere una neurona con
función de activación sigmoide y dos entradas. Grafique la función de la
neurona para w0=0; w1=1; w2=2. Grafique
la línea de frontera
[in1,in2] = meshgrid(-5:.1:5,
-5:.1:5);
alfa=1;
w0=0;
w1=1;
w2=2;
net = w0 + in1*w1 + in2*w2;
z = 1./(1+exp(-alfa*net));
subplot(1,2,1);
mesh(in1,in2,z)
xlabel('in1');
ylabel('in2');
aux = round(z);
subplot(1,2,2);
mesh(in1,in2,aux)
xlabel('in1');
ylabel('in2');
[in1,in2] = meshgrid(-5:.1:5,
-5:.1:5);
alfa=1;
w0=-0.5;
w1=1;
w2=-1;
net = w0 + in1*w1 + in2*w2;
z = 1./(1+exp(-alfa*net));
subplot(1,2,1);
mesh(in1,in2,z)
xlabel('in1');
ylabel('in2');
aux = round(z);
subplot(1,2,2);
mesh(in1,in2,aux)
view(0,90);
xlabel('in1');
ylabel('in2');
w11=-1.1931 w12=-1.1448
w21=-0.9316 w22=-0.9150
b1=0.4107
b2=1.3310
LW1=-1.7003 LW2=1.6087
b3=-0.7221
alfa=4
 |
| Gráfica a |
 |
| Gráfica b |
 |
| Gráfica c |
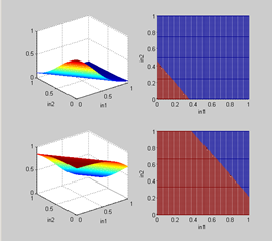
La neurona que se aprecia
en la imagen de la izquierda de la Gráfica b define el punto de inicio de la red
neuronal, es decir que debido a una inversión en su funcionamiento ésta permite
que a la salida de la red neuronal se obtenga una pendiente positiva. La
segunda imagen de la izquierda de la Gráfica b que pertenece a la segunda neurona de la capa
escondida define el punto en donde la función de la red neuronal comienza a
descender, es decir que obtiene una pendiente negativa.
Se puede relacionar esta
red neuronal con la función XOR ya que las dos no son linealmente separables y
necesitan de dos neuronas escondidas para realizar su función correctamente.
Programa:
[in1,in2] = meshgrid(0:.01:1,
0:.01:1);
w11=-1.1931; w12=-1.1448; w21=-0.9316; w22=-0.9150;
b1=0.4107; b2=1.3310; b3=-0.7221;
LW1=-1.7003; LW2=1.6087;
alfa=4;
u1 = b1 + w11*in1 + w21*in2;
z1 = 1./(1+exp(-alfa*u1));
u2 = b2 + w12*in1 + w22*in2;
z2 =
1./(1+exp(-alfa*u2));
net = b3 +
z1*LW1 + z2*LW2;
z = 1./(1+exp(-alfa*net));
subplot(1,2,1);
mesh(in1,in2,z)
xlabel('in1');
ylabel('in2');
aux = round(z);
subplot(1,2,2);
mesh(in1,in2,aux)
view(0,90);
xlabel('in1');
ylabel('in2');
%Para graficar
las líneas de frontera de cada neurona de la capa escondida
figure
subplot(2,2,1);
mesh(in1,in2,z1)
xlabel('in1');
ylabel('in2');
aux1 = round(z1);
subplot(2,2,2);
mesh(in1,in2,aux1)
view(0,90);
xlabel('in1');
ylabel('in2');
subplot(2,2,3);
mesh(in1,in2,z2)
xlabel('in1');
ylabel('in2');
aux2 = round(z2);
subplot(2,2,4);
mesh(in1,in2,aux2)
view(0,90);
xlabel('in1');
ylabel('in2');
7. Determine la ecuación de la línea de frontera y
analice su efecto. Determine el efecto de la variación de w0, w1, w2.
Para la obtención de la
ecuación de la línea de frontera es necesario conocer los pesos que entran
hacia la neurona, lo cual define a la ecuación de la siguiente manera:
Despejando in2, la
ecuación de línea de frontera nos quedaría:
El valor que tenemos de la
relación de w1 con w2 nos permite controlar la pendiente de la línea
de frontera, por otro lado la relación de w0 con w2 nos permite controlar el desplazamiento de la línea
de frontera ya sea hacia la derecha del plano o hacia la izquierda.
